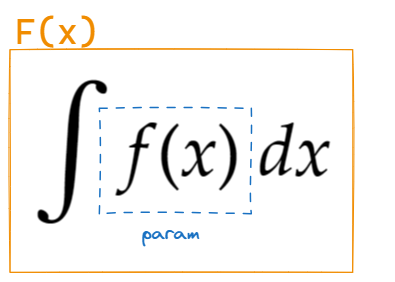有一段时间不看高数了，回来发现又忘记了一大半。想要完全建立一个框架起来，但又总是迷失在细节之中。

还是慢慢串起手中的珠子，能完成多少算多少吧。

微分学

概念

间断点

第一类间断点：可去间断点和跳跃间断点。特点是函数在该点处的左右极限都存在。

第二类间断点：无穷间断点和振荡间断点。特点是至少有一边的极限不存在。

导数根本定义

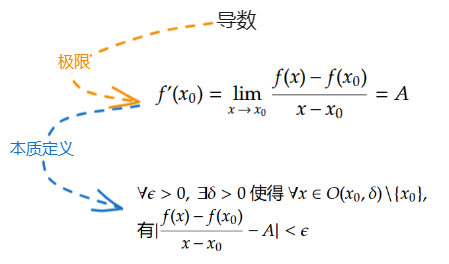
技巧

积分学

概念

定积分的本质定义

设f是[a,b]上的有界函数，

对[a,b]的任意分划 $D: a=x_0<x_1<…<x_n=b$ ，

任取 $\xi_i\in [x_{i-1},x_i]$ 并记 $\Delta x_i=x_i-x_{i-1}$ ，

$\lambda=\max \{\Delta x_i\}\to0$ 时有和式 $\lim \limits_{\lambda \rightarrow 0}\sum \limits_{i=1}^{n}f( \xi_{i}) \Delta x_{i}$ ，

记作定积分 $\int _{a}^{b} f( x) dx$ 。

现考虑变限积分的情况（以 $\int _{a}^{x} f(t) dt$ 为例）。

设f是[a,b]上的有界函数，

对[a,b]的任意分划 $D: a=x_0<x_1<…<x_n=x$ ，

任取 $\xi_i\in [x_{i-1},x_i]$ 并记 $\Delta x_i=x_i-x_{i-1}$ ，

$\lambda=\max \{\Delta x_i\}\to0$ 时有和式 $\lim \limits_{\lambda \rightarrow 0}\sum \limits_{i=1}^{n}f( \xi_{i}) \Delta x_{i}$ ，

记作定积分 $\int _{a}^{x} f(t) dt$ 。

我们发现定义其它部分（包括和式的呈现形式）都并无不同，差异仅在于分划所在的区间。

最后再考虑 $\lambda=\max \{\Delta x_i\}\to0$ 的条件：这意味着 $n\to\infty$ （并不等价，前者是后者的充分条件）。最终归结为，定积分是由数列极限导出的，表现为数列极限求和。上下限只决定分划所在的区间。

变限积分求导

那么，对变限积分的求导何以可能——如果变量甚至只出现在区间上？

不妨再推导一遍变限积分的求导。

求证：

$F'(x)=(\int _{a}^{x} f(t) dt)'=f(x)$ 。

证明：

$F( x+\Delta x) -F( x) =\int _{x}^{x+\Delta x} f( t) dt$ （定义）

$F( x+\Delta x) -F( x) =f(\xi) \Delta x$ （f(x)连续，利用积分中值定理）

（↑积分中值定理的证明见博文原函数、不定积分、定积分关系整理。）

故有 $F'(x)=\lim_{\Delta x\to0}\limits\frac{F(x+\Delta x)-F(x)}{\Delta x}=\lim_{\Delta x\to0}\limits f(\xi)=\lim_{\xi\to x}\limits f(\xi)=f(x)$ 。

这个时候会发现，“沟通了积分和变量的关系”并不能很好地说明积分中值定理最神奇的地方。最有意思的地方在于利用这个定理，我们把区间上的变量挪到了式子中，这得益于函数的连续性所带来的有界性。

Newton-Leibniz公式

设f是[a,b]上的连续函数，F是f在[a,b]上的一个原函数，则 $\displaystyle \int _{a}^{b} f( t) dt=F( b) -F( a)$ 。

证明：

记 $G( x) =\int _{a}^{x} f( t) dt$ ，

由于 $G'(x)=F'(x)=f(x)$ ，恒有 $G(x)-F(x)=C$ 。

也即， $x\in[a,b]$ 时恒有 $\int _{a}^{x} f( t) dt=F(x)+C$ 。

带入特殊值，我们有

$\displaystyle \begin{cases}\begin{aligned}\int _{a}^{a} f( t) dt=F( a) +C=0\end{aligned}\\\int _{a}^{b} f( t) dt=F( b) +C\end{cases}$

两式联立得到 $\int _{a}^{b} f( t) dt=F( b)-F(a)$ 。

有前面的铺垫这个就很好想通，因为看似是两个函数的差，其实是从一个区间中排除另一个区间。

反常积分的敛散性

讨论这一节，首先要把反常积分分为无穷区间和无界函数两种。

无穷区间上的反常积分：

（→） $\int_a^{+\infty}f(x)dx=\lim_{b\to +\infty}\limits\int_a^bf(x)dx$ 存在，则左侧的反常积分存在。
（←） $\int^b_{-\infty}f(x)dx=\lim_{a\to-\infty}\limits\int_a^bf(x)dx$ 存在，则左侧的反常积分存在。
（↔） $\int_{-\infty}^{+\infty}f(x)dx=\int_c^{+\infty}f(x)dx+\int^c_{-\infty}f(x)dx$ ，右侧两个反常积分都收敛时左侧的反常积分收敛。

为什么到了这里需要两个反常积分都收敛呢？本质上，反常积分是定积分的推广，我认为这里是说希望在整个被积的区间上都是可积的，不论是取中间的哪一部分。

再看无界函数的反常积分：

若b是f(x)的唯一瑕点，则无界函数f(x)的反常积分 $\int_a^bf(x)dx$ 定义为 $\int_a^bf(x)dx=\lim_{\epsilon\to0^+}\limits\int_a^{b-\epsilon}f(x)dx$
若a是f(x)的唯一瑕点，则无界函数f(x)的反常积分 $\int_a^bf(x)dx$ 定义为 $\int_a^bf(x)dx=\lim_{\epsilon\to0^+}\limits\int^b_{a+\epsilon}f(x)dx$
若 $c\in(a,b)$ 是f(x)的唯一瑕点，则无界函数f(x)的反常积分 $\int_a^bf(x)dx$ 定义为 $\int_{a}^{b}f(x)dx=\int_a^{c}f(x)dx+\int^b_{c}f(x)dx$ ，右侧两个反常积分都收敛时左侧的反常积分收敛。

总而言之就是挖掉的这个点导致闭区间变成一个或两个开区间，这若干个开区间仍需是可积的。

技巧：不定积分

在写这一块之前我先记录一样东西。

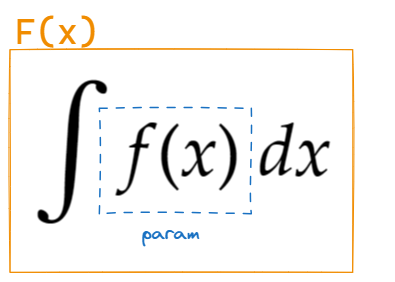
magic_integral

为了看到那个拉长的没有上下标的S时不至于陷入某种空洞的哲学思考，我现在管不定积分号叫这个：求原函数号。

不定积分的积分法有：

第一类换元积分法（凑微分法）
第二类换元积分法
分部积分法

延伸出来还有：

有理函数的积分：部分分式分解
无理函数的积分：换元

有理函数的积分

当我们讨论 $\frac{P_m(x)}{Q_n(x)}$ 的不定积分时，希望将其拆成几个简单分式的代数和。

由代数学基本定理，n次多项式 $Q_n(x)$ 恰有n个根，这n个根或为实数，或为成对出现的共轭复根；由此， $Q_n$ 可分解为若干因数，形如 $(x-a)^k\ (k\geq 1)$ 或 $(x^2+\alpha x+\beta)^k\ (\alpha^2-4\beta\lt0, k\geq 1)$ 。

在 $\frac{P_m(x)}{Q_n(x)}$ 中，前者（因式分解得开）可分解为 $\frac{A_1}{x-a}+\frac{A_2}{(x-a)^2}+...+\frac{A_k}{(x-a)^k}$ ；后者（因式分解不开）可分解为 $\frac{B_1 x+C_1}{x^2+\alpha x + \beta}+\frac{B_2 x+C_2}{(x^2+\alpha x + \beta)^2}+...+\frac{B_k x+C_k}{(x^2+\alpha x + \beta)^k}$ 。

但凡事不要先想不开——遇到分母上为二次的情况，建议是先想想能不能使用凑微分法凑成完全平方+余项的情况。

无理函数的积分

思路是化归为有理函数的积分。好的情况下能去掉分式，坏的情况下能使用有理函数的积分进一步处理。

如果被积函数内形式为 $\sqrt{ax+b}$ ，可直接对它进行换元；

如果根号下次数较高，尝试将它换成分式的形态，比如书上例题的做法

$\int \frac{1}{\sqrt[3]{( x-1)( x+1)^{2}}} dx=\int \frac{1}{x+1}\sqrt[3]{\frac{x+1}{x-1}} dx$

然后对这个分式根式进行换元。

“巧妙的求解技巧”：∫1/(x^4+1)dx

这道题我每次都忘记怎么做，关键它的凑法我自己又根本想不出来，暂时先放在这里供着吧。

$\begin{array}{l} \int \frac{dx}{x^{4} +1}\\ =\frac{1}{2}\int \frac{x^{2} +1}{x^{4} +1} dx-\frac{1}{2}\int \frac{x^{2} -1}{x^{4} +1} dx\\ =\frac{1}{2}\int \frac{1+\frac{1}{x^{2}}}{x^{2} +\frac{1}{x^{2}}} dx-\frac{1}{2}\int \frac{1-\frac{1}{x^{2}}}{x^{2} +\frac{1}{x^{2}}} dx\\ =\frac{1}{2}\int \frac{d\left( x-\frac{1}{x}\right)}{\left( x-\frac{1}{x}\right)^{2} +\left(\sqrt{2}\right)^{2}} -\frac{1}{2}\int \frac{d\left( x+\frac{1}{x}\right)}{\left( x+\frac{1}{x}\right)^{2} -\left(\sqrt{2}\right)^{2}}\\ =\frac{\sqrt{2}}{4}\arctan\frac{}{}\frac{x-\frac{1}{x}}{\sqrt{2}} -\frac{\sqrt{2}}{8}\ln\left| \frac{x+\frac{1}{x} -\sqrt{2}}{x+\frac{1}{x} +\sqrt{2}}\right| +c \end{array}$