考研高数自问自答（三）：多元函数微分篇

今天来探讨多元函数微分的一些问题。从一维推广到多维，函数的各种性质发生了很大变化，需要对原有的研究方法进行扩展。

这次没有以Q&A的方式继续，单纯就几个容易想不清楚的概念进行探究。

多元函数的极限

这里仅给出一般的二元函数，拓展到更多维数或甚至是向量值函数也都很容易，就暂时不写了。

设二元函数 $P_0(x_0, y_0)$ 是D的聚点。如果存在常数A，对于任意给定的正数 $\epsilon$ ，总存在正数 $\displaystyle \delta$ ，使得当点 $\displaystyle P( x,y) \in D\cap \mathring{U}( P_0 ,\delta )$ 时，都有 $\displaystyle | f( x,y) -A| < \epsilon$ ，则称常数A为函数 $\displaystyle f( x,y)$ 当 $\displaystyle ( x,y)\rightarrow ( x_0 ,y_0)$ 时的极限。

注意这样几点：

为什么不再采用 $P_0\in D$ ，而是使用聚点的概念？简单来说，因为我们需要保证它附近总有定义。如果这甚至是个孤立点，是没有办法进行极限的计算的。
当点 $\displaystyle P( x,y) \in D\cap \mathring{U}( P_0 ,\delta )$ 时：点 $M_0$ 的 $\delta$ 去心邻域记作 $\mathring{U}( P_0,\delta )$ 。它的定义为 $\mathring{U}( P_0 ,\delta )=\{M|0\lt\rho(M_0,M)\lt\delta,M\ on \ the \ plane\}$ 。（M在平面上，我也不知道应不应该这么写的）

所以 $\displaystyle ( x,y)\rightarrow ( x_0 ,y_0)$ 的过程如何限定呢？没有限定这条路径怎么走。

我们容易产生一种错觉，好像一维的时候我们就有某种路径的限定，其实是不存在的，只有一个个越套越小的圈；只要在这个收紧的圈里，zig-zag左右横跳也没关系。

二维的情况也是如此，我们只是选取一个又一个更小的 （离散的！） 邻域，选取其中的点，至于这中间的点如何移动，我们不关心也关心不了。正如区间套定理。

或许应当摒弃“（连续）趋向”的数学直觉；从来没有这么定义过（这么多年都是这个定义，不要睁着眼睛乱说）。

全微分和偏导数

在一维的情况下，可微意味着可以采用一阶线性估计。在多元的情况下这一点是一致的，请看：

设n元函数 $\displaystyle u=f( x)$ 在点 $\displaystyle x_0 =\left( x_1^0 ,x_2^0 ,...,x_n^0\right)$ 的某邻域上有定义，如果有一个关于 $\displaystyle \Delta x=( \Delta x_1 ,\Delta x_2,...,\Delta x_n)$ 的线性函数k，使得 $\displaystyle f( x_0 +\Delta x) -f( x_0) =k( \Delta x) +o( \| \Delta x\| )$ ，则称函数f在 $\displaystyle x_0$ 点可微，并称 $\displaystyle k( \Delta x)$ 为f在点 $\displaystyle x_0$ 的全微分，记作 $du$ 。

可微意味着一阶线性估计，故为不同维度上的“以直代曲”。在一维的情况下，可微函数可以被直线局部拟合；在二维的情况下，可微函数可以被平面局部拟合。

可微⟹连续

可微可以推出连续。

设n元函数 $\displaystyle u=f( x)$ 在点 $\displaystyle x_0$ 可微，则f在点 $\displaystyle x_0$ 连续。
证明：
$\displaystyle \exists ( a_1 ,a_2 ,...,a_n) \in \mathbb{R}^n$ ，使得 $\displaystyle \Delta u=f( x_0 +\Delta x) -f( x_0) =a\cdot \Delta x+o( \| \Delta x\| )$
故 $\displaystyle \| \Delta x\| \rightarrow 0$ 时， $\displaystyle \Delta u\rightarrow 0$ ，即f在点 $\displaystyle x_0$ 连续。

（ $\displaystyle \| \Delta x\| \rightarrow 0$ 时， $\displaystyle \Delta u\rightarrow 0$ ：对 $\displaystyle \Delta u$ 使用夹逼法吧！）

偏导数连续⟹可微

导数的定义在多元函数中变成一个很让人头疼的事情，因为我们没办法把向量放到商的位置。怎么办呢？采用各个方向的偏导数所拼凑起来的向量也就是梯度，作为对该点趋向性的表示。

可微也可以推出各个方向的偏导存在：因为向各个轴的线性估计都已给出。各个轴向之间是正交的，是线性无关的，所以求偏导的时候会直接消除其它变量的影响。这里暂且不写了。

但反过来，各个方向的偏导存在并不能推出可微。在某点处诸偏导数的存在性甚至不能保证函数在该点的连续性。如果要举例，考虑一把伞的伞尖，它就是这样的尖点。

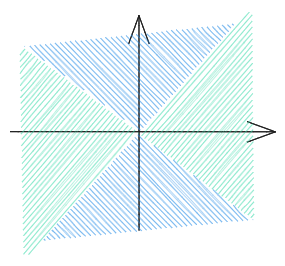
单从偏导数来看是没有问题了——但这个原点处极限不存在（更不用提连续）的函数，怎么可能可微呢？

所以，要推出可微，需要各个方向的偏导连续。尝试证明一下n=2的情况：

注意！偏导数连续也是多元函数连续！注意！偏导数连续也是多元函数连续！注意！偏导数连续也是多元函数连续！

设函数 $\displaystyle u=f( x,y)$ 的偏导数 $\displaystyle \frac{\partial f}{\partial x}$ ， $\displaystyle \frac{\partial f}{\partial y}$ 在点 $\displaystyle ( x,y)$ 连续，欲证f在该点处可微，且 $\displaystyle du=\frac{\partial f}{\partial x} dx+\frac{\partial f}{\partial y}$ 。
考察 $\displaystyle \Delta u=f( x+\Delta x,y+\Delta y) -f( x,y)$ ，

$\Delta u=f( x+\Delta x,y+\Delta y) -f( x+\Delta x,y) +f( x+\Delta x,y) -f( x,y)\\ =f'( x+\Delta x,y+\theta _1 \Delta y) +f'( x+\theta _2 \Delta x,y)$

（Lagrange中值定理）
由偏导数连续得 $\displaystyle \| ( \Delta x,\Delta y) \| \rightarrow 0$ 时，
$f'_x( x+\theta _1 \Delta x,y+\Delta y) = f'_x( x,y) +\alpha$
$\displaystyle f'_x( x,y+\theta _2 \Delta y) =f'_y( x,y) +\beta$

( $\displaystyle \| ( \Delta x,\Delta y) \| \rightarrow 0$ 怎么推出 $\displaystyle \theta_1 \Delta x$ 或 $\Delta y$ 的变化情况？对它使用夹逼法吧）
其中 $\displaystyle \alpha =o( 1)$ ， $\displaystyle \beta =o( 1)$ 。
由此， $\displaystyle \Delta u=f'_x( x,y) \Delta x+f'_{y}( x,y) \Delta y+\alpha \Delta x+\beta \Delta y$
而 $\displaystyle \frac{| \alpha \Delta x+\beta \Delta y| }{\| ( \Delta x,\Delta y) \| } \leqslant | \alpha | +| \beta | =o( 1)$
故 $\displaystyle | \alpha \Delta x+\beta \Delta y| =o( \| ( \Delta x,\Delta y) \| )$
可微得证。