Vanilla Tiramisu's Cookbook

AST有什么用？ AST是沟通语法和语义的桥梁。基于AST，我们可以进行类型检查，进一步进行各种分析等等。 从之前的Parse Tree过渡到AST，我们可以看到发生了如下变化： 可以看到，AST精简了很多，信息也得到了提取。具体而言，它完成了这样几个改进，从而消除了推导过程中的一些步骤和节点： 单一展开形式塌陷，比如factor→value→num→unum 括号等冗余信息被去掉了 运算符和关键字不再被作为叶子结点，比如binOp”+”。 现在，抽象语法树可以被编译器后续编辑干很多事了。 请注意，尽管AST看起来是一棵树，但是它是中间层的一部分，而不是单纯地停留在语法层面，也即它并不是优化的/高级版本的parse tree。 了解了这些，现在可以开始考虑AST的构造方法了。 SDD：语法制导定义 可以使用**语法制导定义（SDD，Syntax Directed Definition）**的方法构造AST，故在此先对语法制导定义做出解释。 语法制导定义能做什么？ 在语义层面，一个拥有合法语义的程序应当满足：类型正确；变量先声明再使用……等等。而这些信息往往是上下文相关的，所以 ...

深度学习的强大在于，它能够从数据中自动学习数据的表示。 什么是机器学习？ 考虑实现这样一个识别狗狗的程序。应当如何实现呢？ 在机器学习中，给定一系列数据，我们不手动地一个个定义输入→输出的映射关系（规则），而是创造一个能通过数据对该映射进行学习的程序。 核心的想法是，如果规则太过复杂/有诸多反例，或甚至于我们不知道规则是什么，那么提供例子还容易些。 识别狗狗的任务感觉可能太复杂，但这其实跟二分类任务差不多：如果在线的下方，就给出⭕，如果在线的上方，就给出❎，在这里这条直线可以由函数x1θ1+x2θ2+θ3≤0x_1\theta_1+x_2\theta_2+\theta_3\leq 0x1​θ1​+x2​θ2​+θ3​≤0得到，我们需要程序学习到θ\thetaθ参数，也就是找到使上述函数正确工作的向量(θ1,θ2,θ3)=θ⃗(\theta_1,\theta_2,\theta_3)=\vec{\theta}(θ1​,θ2​,θ3​)=θ。 接下来问题就在于，怎样进行参数化？换句话说，从狗狗到一系列点/向量，何以可能？ “浅度”学习（Shallow learning） 在回答上面 ...

数分，很神奇吧！ Q： f(x)在[a,b]上可导能否推出f’(x)在(a+ε,b-ε)上连续，其中ε∈(0,b-a)？ 导数极限定理的证明？ 达布定理（导数介值定理）的理解与证明？ A： 函数可导不能推出导数的连续： 考虑函数f(x)={xsin⁡(1x)x≠00x=0f( x) =\begin{cases}x\sin\left(\frac{1}{x}\right) & x\neq 0\\0 & x=0\end{cases}f(x)={xsin(x1​)0​x​=0x=0​ 其导数为f′(x)={2xsin⁡(1x)−cos⁡(1x)x≠00x=0f'( x) =\begin{cases}2x\sin\left(\frac{1}{x}\right) -\cos\left(\frac{1}{x}\right) & x\neq 0\\0 & x=0\end{cases}f′(x)={2xsin(x1​)−cos(x1​)0​x​=0x=0​ 计算lim⁡x→0(2xsin⁡(1x)−cos⁡(1x))\lim_{x\to0}\li ...

修改了结构，方便复习查看；增补了一些内容（Cauchy中值定理的说明）。 Taylor公式推导 Q1：Taylor公式如何推导？有什么用？ Taylor公式： 我们希望使用一个n次多项式来拟合一个函数f的行为： a0+a1(x−x0)+...+an(x−x0)n+o((x−x0)n)a_0+a_1(x−x_0)+...+a_n(x−x_0)^n+o((x−x0)^n)a0​+a1​(x−x0​)+...+an​(x−x0​)n+o((x−x0)n) 构造这个多项式的用意在哪里呢，在于拿它和f作差之后剩下的是一个比(x−x0)n(x-x_0)^n(x−x0​)n高阶的无穷小。由此，我们可以利用这个思路来得出中间每一项的系数，最终就会得到： f(x)=∑k=0n1k!f(k)(x0)(x−x0)k+o((x−x0)n)f(x)=\sum\limits_{k=0}^n\frac{1}{k!}f^{(k)}(x0)(x−x0)^k+o((x−x0)^n)f(x)=k=0∑n​k!1​f(k)(x0)(x−x0)k+o((x−x0)n) 写下最上面的多项式的时候我突然想到，这个式子非常有 ...

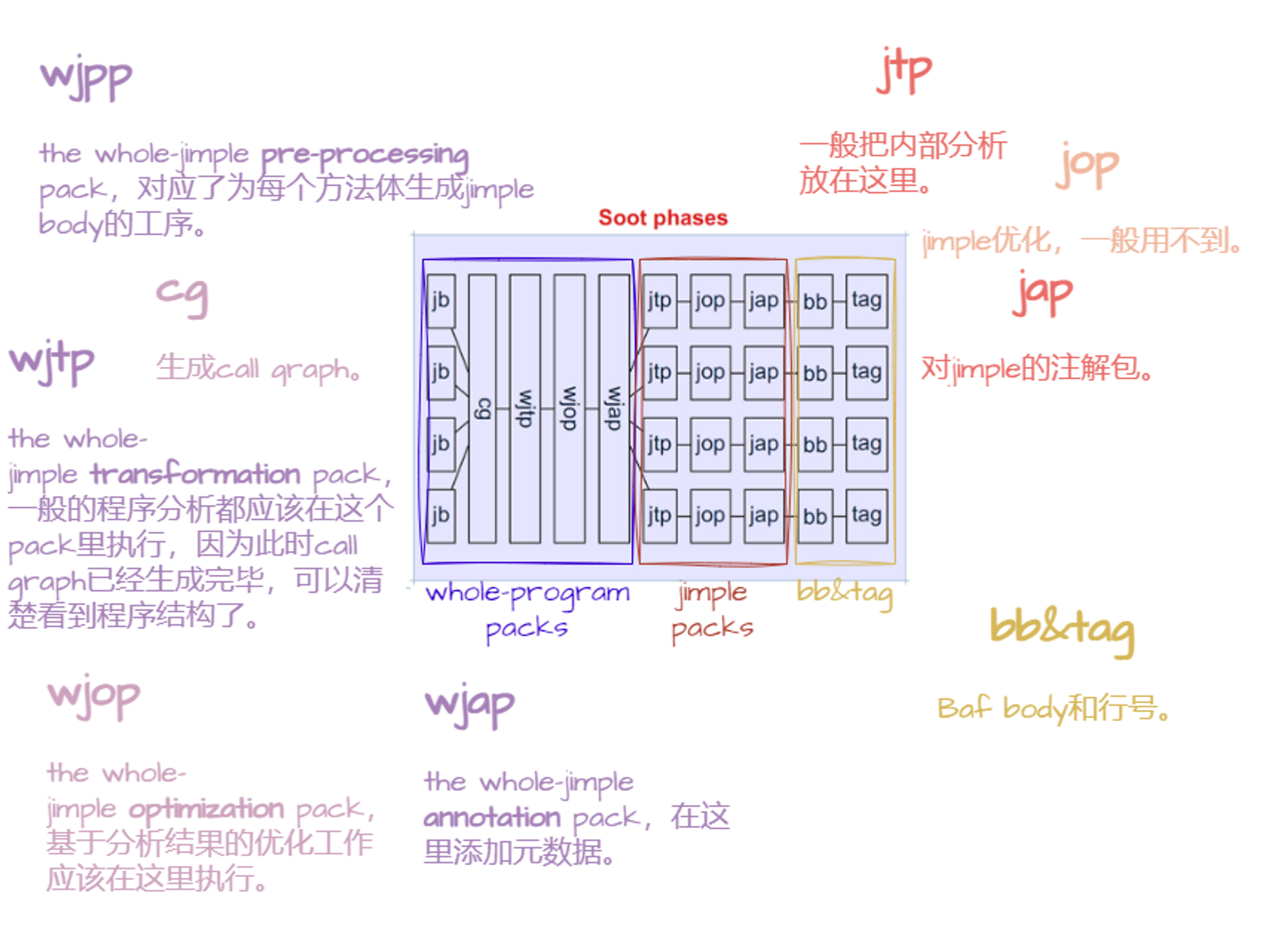
这段时间在学习使用Soot和FlowDroid进行静态分析，但苦于没有学过静态分析的知识，而文档和资料又太简陋（点名批评FlowDroid），对初学者非常不友好，所以尝试记录一些Soot和FlowDroid的知识，会持续更新。 Soot Soot在不同阶段完成不同的工作，我们要做的只是在某些特定阶段添些工序，也就是加到待执行的任务集packs中。 FlowDroid FlowDroid用于分析数据的source和sink，它可以有效剪去部分不会执行的路径，并且对于Android app，FlowDroid根据Android生命周期特别地进行了优化和抽取。它是基于Soot的封装，所以其分析基于Jimple进行。 给定source和sink，FlowDroid会采用IFDS算法进行求解，得到这两点之间所有可能的路径。此外，FlowDroid也包含一些其他组件，用以处理各种问题，比如Entry Point Creator会在不知道主要入口点（从而在生成call graph无从下手时）生成一个dummy entry point来解决问题。 参考资料（部分） 移动应用安全常用组件Soot、F ...

Welcome to Hexo! This is your very first post. Check documentation for more info. If you get any problems when using Hexo, you can find the answer in troubleshooting or you can ask me on GitHub. Quick Start Create a new post 1$ hexo new "My New Post" More info: Writing Run server 1$ hexo server More info: Server Generate static files 1$ hexo generate More info: Generating Deploy to remote sites 1$ hexo deploy More info: Deployment